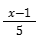קיץ 2023 כמותי 1

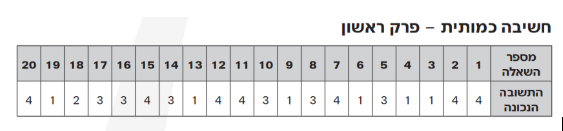
1. “אם נחלק את קו המשווה ל-80 קטעים שאורכיהם שווים זה לזה, מה יהיה אורכו של כל קטע (בקירוב?)”
   תשובה (4) נכונה
   זיהוי: שאלה כללית (על דרך השלילה, זו שאלה שלא מתאימה לשום שאלה אחרת)
   כלים רלוונטיים: הערכת סדר גודל
   תשובות: במספרים, ומספרים שונים בעיקר בספרת המאות.
   פתרון: נותנים לנו מספר גדול ומכוער, ורוצים שנחלק אותו פחות או יותר ב-80. אנחנו נעבוד הפוך! נלך לתשובות ונבדוק באיזו אחת הכפלה ב-80 תביא אותנו קרוב ל40,000. נבדוק את זה באמצעות ספרת המאות בלבד!
   1. __1×80 = 80
   2. __2×80 = 160
   3. __3×80 = 240
   4. __5×80 = 400 – היחידה שמסתדרת עם התשובה שלנו!
2. תשובה (4) נכונה
   זיהוי: משוואות
   כלים רלוונטיים: פישוט קלאסי
   תשובות: בנעלמים עם שברים. לא נוח להציב תשובות.
   פתרון: נתונה המשוואה x – 5y = 1 נעבוד אלגברית ונבודד את y:
   1. נוסיף 5y ל2 אגפי המשוואה כדי לקבל: x = 1+ 5y
   2. נוריד 1 משני אגפי המשוואה כדי לבודד את הy: x – 1 = 5y
   3. נחלק את שני האגפים ב-5:  y =
3. תשובה (1) נכונה
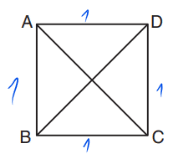
   שאלת גיאומטריה – שרטוט: יש לנו ריבוע שמחולק ל4 משולשים, ללא נתונים.

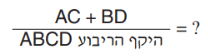
            שאלה: 
            תשובות: כולן בשברים. תשובות (1) ו(2) מרמזות לנו באמצעות 2,3 על משולשי סמי ודוגמנית
            פתרון: כשאין נתונים בשרטוט – נוכל להציב מספרים נוחים בשרטוט! AC ו-BD הם אלכסונים, אז נעדיף להציב באחת מצלעות הריבוע ולעבוד משם באמצעות פיתגורס:

1. 1. נציב 1 בצלעות הריבוע – מכאן אפשר לראות שההיקף הוא 4: 
2.                

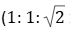
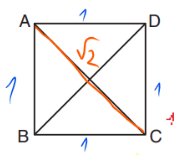
                   2. מכאן נחשב את האלכסון באמצעות יחס צלעות במשולש סמי (משולש ישר זווית שווה שוקיים המקיים את יחס הצלעות  -נשים לב שהחישוב גם

                          נותן לנו את BD מכיוון שאלכסונים בריבוע שווים:

                   3. נציב את הנתונים שמצאנו בשאלה: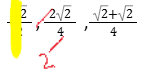

                   4. תשובה (1) נכונה
                        זיהוי: הכל בדולר
                        כלים רלוונטיים: ניסוח הפעולה במילים שלנו, סדר פעולות חשבון
                        תשובות: בנעלמים, מה שמרמז לנו שאפשר להציב מספרים מהראש (אבל צריך להיזהר מזה, כי התרגיל מורכב בעיקר מחזקות, אז יש סיכוי גבוה לכמה תשובות נכונות/מספרים ממש גבוהים)
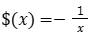
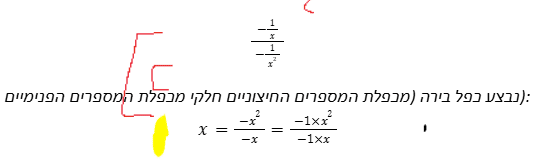
                        פתרון: נעבוד אלגברית. נגדיר את הפעולה במילים שלנו: מחלקים את 1 ב – X, ומוסיפים מינוס לפני. נחיל את הפעולה על המונה והמכנה של השאלה:

          תשובה (3) נכונה
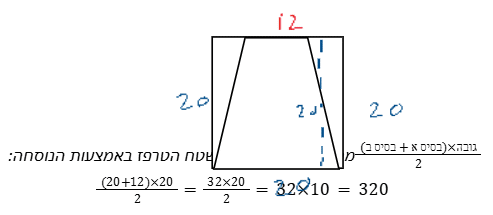
                          שאלת גיאומטריה – שרטוט: אין שרטוט, אבל מדברים על ריבוע שבתוכו חסום טרפז אז נשרטט.
                          שאלה: מהו שטחו המקסימלי של הטרפז? (מכאן אפשר להסיק שנצטרך את נוסחת שטח הטרפז)
                                      תשובות: במספרים, לא אומרים לנו יותר מדי.
פתרון: נשתמש בנתונים כדי לשרטט. נתון ששטחו של הריבוע הוא 400 סמ”ר, אז נוכל לחשב את צלעו: 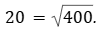 נתון שהבסיס הקטן של הטרפז הוא 12 ס”מ, אז השרטוט יראה כך:

                      5. אחוז פריטי הלבוש בארון של גילה שצבעם כחול הוא לכל הפחות ___ ולכל היותר ____.
                           תשובה (1) נכונה
                           זיהוי: כללית ואחוזים – מינימום מקסימום. (שואלים אותנו על לכל הפחות ולכל היותר והתשובות באחוזים)
                           פתרון: שואלים אותנו על פריטי הלבוש שבצבע כחול מתוך 50 פריטי לבוש. נתחיל בלחשב את המינימום: נתון ש10 חולצות הן בצבע כחול, ואין נתונים מגבילים אחרים. אז המינימום הוא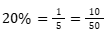
                           כדי לחשב את המקסימום נחשב את החולצות והחצאיות בנפרד. חולצות = נתון ש10 בלבד כחולות. בחצאיות נתון ש5 בלבד חומות = מה שמותיר 20 שיכולות להיות כחולות.
                           בסה”כ יש 30 פריטים: 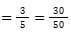60%. בסה”כ הטווח הוא 20%-60%.

                      6. איזה מרצפי הצבעים הבאים הוא בעל הסיכוי הנמוך ביותר להיות הרצף שירשום נמרוד על הדף?
                          תשובה (4) נכונה
                          זיהוי: הסתברות (שואלים על סיכוי של משהו)
                         כלים רלוונטיים: מצוי/רצוי = מה הסיכוי, רצף של אירועים.
                         תשובות: ברצפים של אירועים – נשים לב שכולם באותו אורך (6), ושיש אופציה שלכולם אותה הסתברות.
                         פתרון: נתחיל בלחשב את ההסתברות של כל צבע. שחור
                         מכיוון שההסתברויות שוות, וכל הרצפים באותו אורך, אז אין הבדל בין ההסתברויות! כולן יהיו:                                                                         

                   7. כמה פתרונות יש למשוואה x2–x=0?
                       תשובה (3) נכונה
                       זיהוי: חיובי שלילי (ערך מוחלט)
                      כלים רלוונטיים: פישוט קלאסי, הצבת מספרים מהראש.
                      פתרון:

                                   1. נתחיל מפישוט קלאסי – נוסיף  | x |  לשני אגפי המשוואה: | x² =| x

                                   2. בשני הצדדים יש משהו שהופך הכל לחיובי, אך החזקה גם יכולה לשנות את הערך המספרי. נציב מספרים קטנים (נתחיל מ-0) ונראה איזה מהם פותרים את המשוואה: | 0 | = 0² ⇐ 0 = 0 פתרון ראשון.

                                   3. | 1 | = 1² ⇐ 1 = 1 פתרון שני.

                                   4. | 2 | = 2² ⇐ 2 = 4 לא עובד (תשובה 4 נפלה). נעבור למספרים שליליים:

                                   5. | 1 – | = ²(1 – ) ⇐ 1 = 1 פתרון שלישי.

                    8. כמה גולות יש למירב?
                        תשובה (1) נכונה
                        זיהוי: ממוצע (“…שווה למספר הגולות שיש בממוצע לכל אחת מהן”)
                       כלים רלוונטיים: נוסחת הממוצע 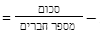 סכוםחברים מספר  = ממוצע.
                       תשובות: מספרים קטנים יחסית.
                       פתרון א’: אלגברית. 

                                     1. נסמן את יפעת ומירב באותיות מייצגות וניצור משוואה ראשונה מהנתון שמספר הגולות של שניהן ביחד הוא 48: y + m = 48

                                     2. ניצור משוואה שנייה מהנתון שההפרש ביניהן שווה לממוצע. הממוצע הוא 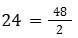 אז המשוואה היא y – m = 24 (נשים לב שY ראשון כי נתון שליפעת יש יותר גולות ממירב).

                                     3. נבצע חיסור משוואות בין 2 המשוואות שמצאנו: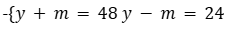

                                     4. חלק את המשוואה שקיבלנו –  2m = 24 ב-2: m = 12

                    9. מה סכום השטחים הכהים?
                        תשובה (3) נכונה
                        שאלת גיאומטריה – שרטוט: יש לנו משולש ישר זווית עם 2 משולשים שחורים ומשולש לבן – מה שמרמז לנו על חיבור וחיסור שטחים.
                        שאלה: רוצים מאתנו את השטח של המשולשים.
                        תשובות: במספרים, אבל אין ממש מה לעשות איתם.
                        פתרון: נשתמש בנתון שABC שווה שוקיים כדי לחשב את שטח המשולש הגדול, וממנו נוריד את המשולש הלבן:

                                     1. נחשב את שטח המשולש הגדול: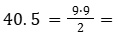  

                                     2. נחשב את שטח המשולש הלבן: הבסיס שלו נתון, והגובה שלו הוא בעצם בסיס המשולש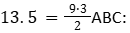

                                     3. נחסר את המשולש הלבן מהגדול = 13.5 – 40.5 = 27

                 10. ערכו של איזה מהביטויים הבאים הוא הגדול ביותר?
                        תשובה (4) נכונה
                        זיהוי: אי שוויון
                       כלים רלוונטיים: חוקי אי שוויונים, הצבות.
                       תשובות: נעלמים (מרמז על הצבת מספרים מהראש) בחזקות ושורשים.
                      פתרון: נציב מספרים נוחים שיקיימו את אי השוויון, ונציב אותם בתשובות.

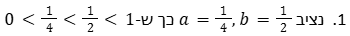
                 11. על פי נתונים אלו והנתונים שבסרטוט, γ= ?
                       תשובה (4) נכונה
                       שאלת גאומטריה – שרטוט: יש כאן הרבה ישרים, וזוויות α,β,γ.
                       תשובות: יש נעלמים, כך שאפשר לנסות להציב מספרים מהראש.
                      פתרון: נעזר בנתונים – יש לנו כאן כמה ישרים מקבילים, ככה שהעבודה תהיה באמצעות צורות מוכרות וזוויות.

                                                1. נשלים את הזווית α על הישר a:

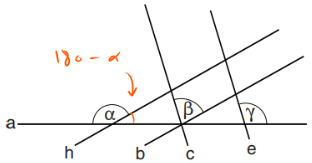
                                              2. נזהה את הזורו ונמלא את הנתונים על הזוויות הקודקודיות:

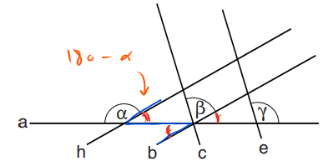
                                            3. נזהה את הצורה של זוויות מתאימות כך ש – γ = 180 + β – α:

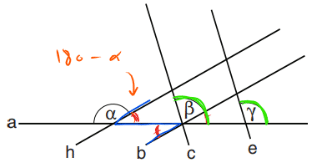
                 12. כמה ימים יצטרך רפי לעבוד כדי לבצע עבודה שאימו מבצעת ב-6 ימים?
                        תשובה (1) נכונה
                        זיהוי: שאלת הספק (מדברים על ההספק של רפי ושל אימא שלו)
                        כלים רלוונטיים: סוג שאלת הספק – פועל בודד (כל אחד עובד בנפרד), יחסים בהספק.
                        תשובות: במספרים נוחים, ונשתמש בהם.
                       פתרון:
                       דרך א’: מתחכמת – בנתון הראשון כתוב לנו שביום אחד רפי עובד חצי מהזמן שאימא שלו עובדת. לפי יחסים בהספק, אם נעבוד בחצי מהזמן ייקח לנו פי 2 זמן. אז לפני שנשלים את הנתונים האחרים נוכל להסיק שייקח לו 12 ימים. הנתון השני אומר לנו שההספק שלו קטן מההספק של אמו. זה אומר שייקח לו יותר זמן: תשובות (2) (3) (4) נופלות.
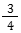
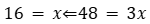
                      דרך ב’: הצבת מספרים מהראש – נציב בהספק של אימא 4 ונחליט שהיא עובדת 2 שעות. מכאן אפשר לחשב את העבודה שהיא תבצע בסה”כ – 6 ימים × 2 שעות × 4 הספק = 48 עבודה בטוטאל. רפי יעבוד בהספק של כך שהספקו בפועל יהיה 3, וזמן העבודה שלו בכל יום הוא מחצית משל אמו כך שיעבוד שעה 1 בכל יום. נציב במספר הימים X כי על זה שאלנו אותנו: 3 הספק × 1 שעות × X ימים = 48 עבודה בטוטאל.

                13. מה המספר הגדול ביותר אשר M+L+K מתחלק בו בהכרח ללא שארית?
                      תשובה (3) נכונה
                      זיהוי: חלוקות (שואלים מה מתחלק בהכרח)
                      תשובות: כולן כפולות של 3, אבל זה לא עוזר במיוחד.
                     פתרון: נציב מספרים שונים מהראש ונראה אם נוכל לפסול תשובות. אם כל אחד מהנעלמים מתחלק ב-3, אין צורך לבדוק את 3 – זה תמיד יהיה נכון😊 (שימו לב שאם נציב 0 באחד המספרים זה יהיה מהיר הרבה יותר, אך כאן החלטנו להראות דרך מעט יותר ארוכה).

1. 1. נציב 9+6+3 = 18. 18 אינו מתחלק ב-12 ולא ב-15. תשובות (1) ו-(2) נפלו.
   2. נציב 3+6+12 = 21. 21 אינו מתחלק ב-6. תשובה (4) נפלה.

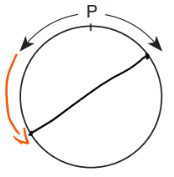
               14. מה הדרך (בק”מ) שעבר נועם עד לרגע זה?
                      תשובה (4) נכונה
                      זיהוי: שאלת תנועה (משהו זז במרחב במהירות ובזמן מוגדרים)
                      כלים רלוונטיים: טבלת מז”ד, יחסים בתנועה.
                      תשובות: כולן ב-π, אבל לא מעניינות במיוחד.
                     פתרון:

                                  1. נבין היכן הייתה הנקודה הראשונה שבה הם היו שניהם על הקוטר:

                                 2. נחשב את הדרך ששניהם עשו בסה”כ באמצעות חישוב חצי היקף המעגל:  

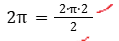
                                 3. נוכל לפסול את תשובות (1) שנראה ממנה שהם עברו את אותה דרך ואת תשובה (2) שנראה ממנה שנועם היה היחיד שזז.

                                 4. מכיוון שהיחס בין המהירויות של נועם וריקי הוא 1:2, נחלק את הדרך ב3 כדי למצוא את המרחק המדויק שכל אחד מהם נע: יש לנו 3 מקטעים של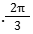

                                 5. יש יחס ישר בין מהירות לדרך – ולכן נועם עשה 2 מקטעים של

 גרף

                15. מתן נוסע באוטובוס האחרון מיישוב D אל העיר. הוא מעוניין לנסוע עוד באותו ערב באוטובוס נוסף מן העיר אל אחד משלושת היישובים האחרים, וללון שם.
בכמה משלושת היישובים האחרים יוכל לבחור?
תשובה (3) נכונה
פתרון: האוטובוס האחרון מיישוב D יוצא ב21:00, ומשך הנסיעה שלו הוא 55 דק’, אז מתן מגיע בפועל אל העיר בשעה 21:55. נבדוק בגרף כמה אוטובוסים יוצאים ליישובים האחרים:
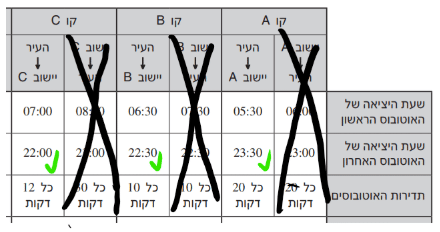
יש לו 3 אופציות! תשובה (3) נכונה

1.  בכל קו מוגדרת “כדאיות הנסיעה” כך:
   כדאיות הנסיעה בקו ____ היא הגדולה ביותר.
   תשובה (3) נכונה
   פיתרון: נשתמש בנתונים על המשך והמחיר ונבדוק (בקירוב):
   1. 2=4017 בקירוב
   2. 3=309 בקירוב
   3. 3.5=3510 בדיוק!
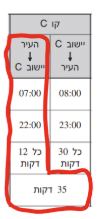
   4. 2.5=5522 בקירוב
2. דליה רוצה לנסוע מן העיר אל יישוב C. אם היא רוצה להגיע אל היישוב לכל המאוחר בשעה 16:30, האוטובוס המאוחר ביותר שהיא יכולה לנסוע בו יוצא בשעה –
   תשובה (2) נכונה
   פתרון: נבדוק כל כמה זמן יוצא אוטובוס מהעיר אל יישוב C:
   אם הקו יוצא בשעה עגולה (07:00), ויוצא כל 12 דק’, אז הוא יוצא
   ב12 דק’ לשעה, ב24 דק’, ב36 וב48 ואז שוב בשעה עגולה. כך
   שתשובות (3) ו(4) נופלות. כדי להגיע בזמן, דליה צריכה לצאת 35 דק’
   לפני 16:30 – כלומר ב15:55. תשובה (2) מסתדרת!
   
   
   
   
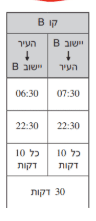
3. בקו B, כמה אוטובוסים מצויים במהלכה של נסיעה בשעה 18:23 בכל יום?
   תשובה (1) נכונה
   פתרון: נבדוק את תדירות יציאת האוטובוסים של קו B, ואת זמן נסיעתם:
   האוטובוסים יוצאים בכל 10 דקות בשעות עגולות (06:30, 06:40) וכו’, אז
   נתקדם לשעה הרלוונטית. הקווים הכי מתקדמים בנסיעה שלהם יהיו
   ה-2 שהתחילו את נסיעתם ב18:00 (הם 23 דק’ לתוך הנסיעה). אחריהם
   יהיו עוד 2 אוטובוסים שהתחילו את נסיעתם ב18:10 ועוד 2 אוטובוסים
   שהתחילו את נסיעתם ב18:20.
   
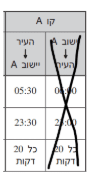
4. כמה פעמים ביום יוצא אוטובוס מן העיר אל יישוב A?

תשובה (4) נכונה

פתרון: נסתכל בגרף על הנתונים של קו A מהעיר ליישוב: היציאה הראשונה
היא ב05:30, והאחרונה היא ב23:30 – לאחר 18 שעות. הוא יוצא כל 20
דקות, כך שבכל שעה יש 3 אוטובוסים שיוצאים. נחשב 18×3 = 54. לאן

נעלם 1? כי אנחנו צריכים לספור גם את האוטובוס שיוצא בתחילת השעה
23:30 (לא כלול בחישוב). ביחד איתו יש 55 אוטובוסים בסה”כ.