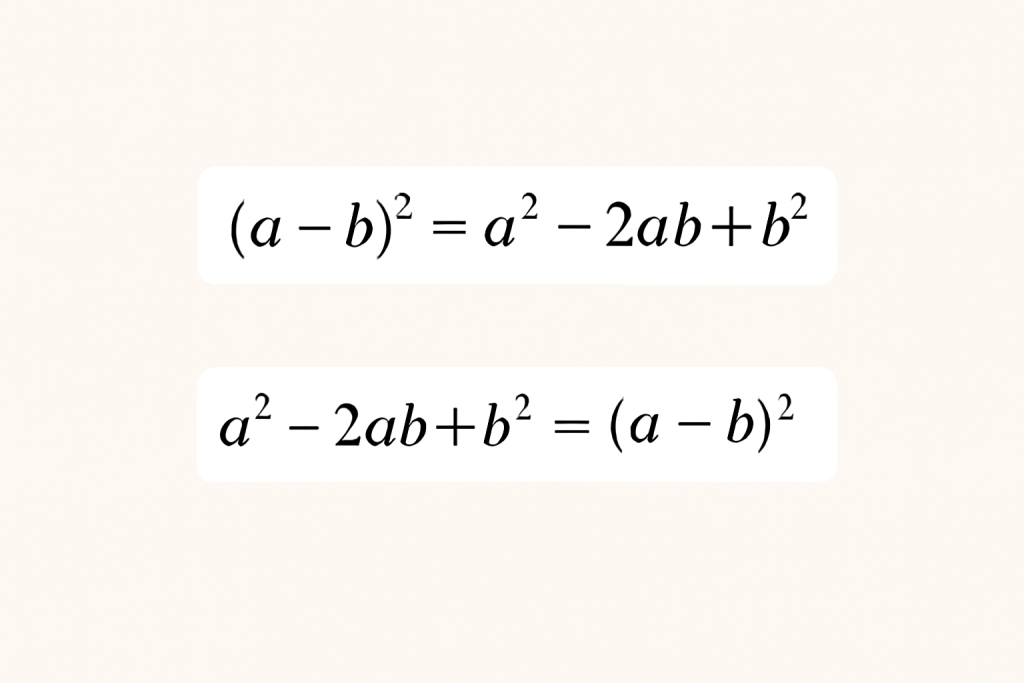נוסחאות הכפל המקוצר הן אחד הכלים המרכזיים באלגברה, ובמיוחד כשהן מופיעות בפסיכומטרי. כל נוסחה מאפשרת לנו לבצע פעולות מתמטיות בצורה פשוטה ומהירה, ומסייעת לנו לפתור בעיות מורכבות בלי להסתבך. המאמר הזה יתמקד בנוסחה השנייה לכפל המקוצר, שהיא נוסחת ריבוע ההפרש – ונראה איך מפרקים ומרכיבים אותה בצורה יעילה.
נוסחת הכפל המקוצר השנייה – ריבוע ההפרש
הנוסחה השנייה בכפל המקוצר מתייחסת ל-ריבוע ההפרש של שני איברים:
(a−b)2=a2−2ab+b2(a – b)^2 = a^2 – 2ab + b^2(a−b)2=a2−2ab+b2
איך נראית הנוסחה?
- a^2 – ריבוע של האיבר הראשון
- -2ab – כפול שני האיברים והמכנה 2
- b^2 – ריבוע של האיבר השני
דוגמה:
נניח שאנחנו רוצים לפתח את הביטוי (x−4)2(x – 4)^2(x−4)2:
(x−4)2=x2−2⋅x⋅4+16=x2−8x+16(x – 4)^2 = x^2 – 2 \cdot x \cdot 4 + 16 = x^2 – 8x + 16(x−4)2=x2−2⋅x⋅4+16=x2−8x+16
הנה איך זה עובד:
- x^2 הוא ריבוע האיבר הראשון (x)
- -8x הוא הכפל של האיבר הראשון עם האיבר השני, כפול 2 (2×4 = 8)
- 16 הוא ריבוע האיבר השני (4^2 = 16)
פירוק והרכבה של הנוסחה
כעת נלמד איך מפרקים ומרכיבים את ריבוע ההפרש.
איך מפרקים את הביטוי?
אם יש לכם ביטוי כמו x2−8x+16x^2 – 8x + 16×2−8x+16, תוכלו להחזיר אותו בצורה של ריבוע ההפרש.
- חפשו את האיבר האמצעי: במקרה הזה, האיבר האמצעי הוא -8x.
- חלקו אותו ב-2 (כמו בנוסחה):
−82=−4\frac{-8}{2} = -42−8=−4 - צרו את הנוסחה:
(x−4)2(x – 4)^2(x−4)2
דוגמה:
נניח שיש לנו את הביטוי x2−10x+25x^2 – 10x + 25×2−10x+25.
- נזהה את האיבר האמצעי: -10x
- נבצע את החלוקה ב-2:
−102=−5\frac{-10}{2} = -52−10=−5 - כעת נרכיב את הנוסחה:
(x−5)2(x – 5)^2(x−5)2
הנה איך אפשר להחזיר את הביטוי לפורמט של ריבוע ההפרש.
כיצד לבצע פירוק והרכבה של ריבוע ההפרש
| שלב 3
הרכיבו את הנוסחה |
שלב 2
חלקו ב-2 |
שלב 1
חפשו את האיבר האמצעי |
ביטוי |
| (x−4)2(x – 4)^2(x−4)2 | -4 | -8x | x2−8x+16x^2 – 8x + 16×2−8x+16 |
| (x−5)2(x – 5)^2(x−5)2 | -5 | -10x | x2−10x+25x^2 – 10x + 25×2−10x+25 |
| (y−6)2(y – 6)^2(y−6)2 | -6 | -12y | y2+12y+36y^2 + 12y + 36y2+12y+36 |
למה זה חשוב לפסיכומטרי?
בפרק הכמותי של הפסיכומטרי, הכרת נוסחאות הכפל המקוצר, ובעיקר את נוסחת ריבוע ההפרש, תעזור לכם:
- לחסוך זמן רב בשאלות שמבוססות על פיתוח ביטויים.
- לפשט שאלות שמכילות חזקות וצריכות הפיתוחים הללו.
- לפתח פתרון מהיר ומדויק, בלי לגלות טעויות בדרך.
היתרון הוא שאתם יכולים להפעיל נוסחה אחת כדי להימנע מפתרון ארוך ומסובך.
איך לומדים את זה בזינוק?
בקורס הפסיכומטרי של זינוק, אנחנו מלמדים איך לזהות את ריבוע ההפרש, איך לפרק ולהרכיב ביטויים בצורה חכמה וממוקדת. התרגול האינטנסיבי שלנו נותן לכם את הכלים הכי יעילים לא רק כדי לפתח ביטויים, אלא גם כדי לחשוב בצורה מהירה ונכונה בזמן המבחן.
- תוכנית לימוד מותאמת אישית לכל תלמיד.
- כיתות קטנות עם ליווי צמוד.
- תרגולים ממוקדים והסברים ברורים שמאפשרים שליטה מלאה.
שאלות ותשובות נפוצות
- מה ההבדל בין ריבוע סכום לריבוע הפרש?
ריבוע סכום כולל תוספת של 2ab בעוד שריבוע הפרש כולל חיסור של 2ab. - איך אני יודע מתי להשתמש בנוסחת ריבוע ההפרש?
אם יש לכם שני ביטויים בתוך סוגריים (אחד עם פלוס והשני עם מינוס), וידוע לכם שהם זהים – אתם יכולים להשתמש בנוסחה. - האם אני חייב ללמוד את הנוסחאות בעל פה?
למדו את הנוסחאות, אך מה שיותר חשוב זה להבין את ההיגיון שלהן – זה יקל עליכם בשלב הפתרון. - איך אני יכול לדעת אם ביטוי הוא ריבוע הפרש?
אם אתם רואים סכום ומינוס בין שני איברים, תבדקו אם הם זהים – זה סימן לכך שניתן להשתמש בנוסחה. - האם זינוק מלמד את זה בקורסים?
כן! בזינוק אנו מלמדים את כל נוסחאות הכפל המקוצר בהבנה עמוקה ומסבירים איך לזהות אותן במהלך הבחינה.
סיכום – שליטה בנוסחת ריבוע ההפרש = יתרון ייחודי
נוסחת ריבוע ההפרש היא אחת הכלים החשובים ביותר במתמטיקה, במיוחד בפסיכומטרי. השליטה בה לא רק הופכת את פתרון השאלות למהיר ויעיל, אלא גם חוסכת זמן יקר, שיעזור לכם לפתור את יתר השאלות בזמן.
אם אתם רוצים ללמוד איך לשלוט בנוסחאות כמו מקצוענים – הצטרפו עכשיו לקורס הפסיכומטרי של זינוק.