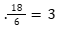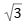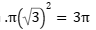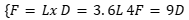קיץ 2023 כמותי 2

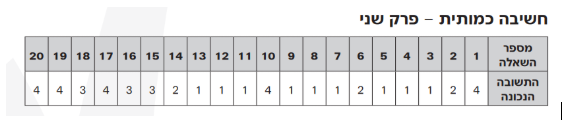
1. “כמה סוכריות היו לכל קבוצה?”
   תשובה (4) נכונה
   זיהוי: שאלת ממוצע (לא נאמר במפורש, אך יש סכום שמחלקים באופן שווה בין מספר חברים)
   כלים רלוונטיים: נוסחת הממוצע
   תשובות: במספרים, ומספרים שונים בעיקר בספרת המאות.
   פתרון: אומרים לנו שיש 7 ילדים, וכל אחד מקבל סוכריה אחת יותר מהשני. אז נסכום את כל הסוכריות: 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28. נחלק את המספר הזה ל2 קבוצות ונקבל שכל קבוצה קיבלה 14.
2. תשובה (2) נכונה
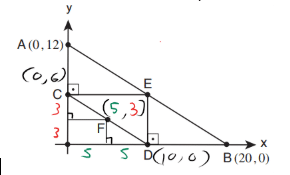
   שאלת גיאומטריה – שרטוט: יש לנו מע’ צירים, ובתוכה הרבה משולשים ישרי זווית.
   שאלה: מהם ערכי הנקודה F?
   תשובות: במספרים.
   פתרון: נתון לנו שהנקודות E ו-F הם אמצעי הקטעים של AB ו-CD בהתאמה. מכיוון ש-CE יוצא מאמצע קטע ומקביל לבסיס של המשולש (בגלל הזווית הישרה) אז הוא קטע אמצעים ושווה למחצית מהבסיס. אותו הדבר נכון לקטע DE.  נשתמש בנתונים אלו כדי להשלים את הנתונים:

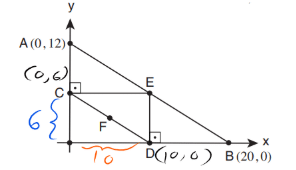
            מכאן, אפשר להשתמש בבניית עזר וליצור שני קטעי אמצעים חדשים המגיעים לנקודה F ובכך למצוא את שיעורי הנקודות:

           

        3. מה הערך הקטן ביותר האפשרי של הביטוי x-y)²)?
            תשובה (1) נכונה
            זיהוי: ביטויים
            כלים רלוונטיים: הצבת מספרים מהראש
            תשובות: במספרים קטנים ויפים.
            פתרון: נתון לנו שX ו-Y הם שלמים שונים זה מזה. אז נציב את המספרים הכי קטנים שנוכל:

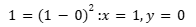
          תשובות (2) ו(4) נפלו. עכשיו נפעיל היגיון אלגברי: כדי לקבל 0 בתרגיל חיסור שבסוגריים, הדרך היחידה האפשרית היא כששני הנעלמים שווים זה לזה(x=y⇐x-y=0). אך נתון לנו שזה לא המצב ולכן תשובה (3) נפסלת. תשובה (1) נכונה.

        4. איזה מהביטויים הבאים יכול לבטא את דרגת הקושי של פאזלים?
            תשובה (1) נכונה
            זיהוי:  שאלה כללית (על דרך השלילה – אין כאן תבנית מוכרת)
            פתרון: נתון כי לנו כי ככל ש-N יותר גבוה רמת הפאזל עולה, וכל ש-C יותר נמוך רמת הפאזל עולה. נלך לתשובות ונראה מה מתאים:

 יש לנו כאן שבר מהנעלמים. ידוע כי ככל שהמונה עולה והמכנה יורד, התוצאה גדלה. ההתנהגות הזאת מתאימה לנעלמים שקיבלנו ולכן התשובה נכונה!

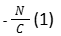
 (2) N⋅C – הביטוי אינו מתאים, היות ורמת הקושי יכולה לעלות גם כשN נמוך וC גדל.

(3) N + C – כמו בתשובה הקודמת, הביטוי אינו מתאים היות ורמת הקושי יכולה לעלות גם כשN נמוך וC גדל.

(4 )C – N   – כאן יקרה המקרה ההפוך. ככל שN יהיה גדול יותר וC יהיה קטן יותר, התוצאה תקטן.

        5.
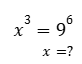
             תשובה (1) נכונה
             זיהוי: משוואות – חזו”ש (תבנית עם חזקות)
             כלים רלוונטיים: חוקי חזקות, הצבת תשובות
             תשובות: במספרים, עם חזקות.
            פתרון: נבצע הצבת תשובות:

        6. הצלע שמול הזווית שגודלה 3α גדולה פי ____ מהצלע שמול הזווית שגודלה α.

             תשובה (2) נכונה
             גאומטריה – שרטוט: אין שרטוט. מדברים על זוויות במשולש.
            פתרון: אומרים לנו שהזוויות הן α, 2α ו-3α. היחס הזה מתאפשר רק במשולש דוגמנית שזוויותיו הן 30:60:90. הצלע שמול הזווית  הגדולה (היתר) גדולה פי 2 מהצלע שמול הזווית הקטנה (הניצב הקטן). תשובה (2) נכונה.

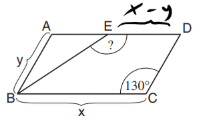
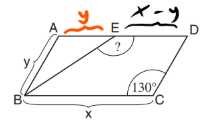
       7. ?= BED∡ 
           תשובה (1) נכונה
           גאומטריה – שרטוט: יש כאן מקבילית עם צלעות בנעלמים וזווית נתונה. זה מוביל אותנו למחשבה על זוויות.
          שאלה: רוצים את זווית BED.
          תשובות: במספרים דומים.
          פתרון: 

                        1. בנתונים רשום ש – ED = x – y. נשלים את הנתונים בשרטוט שלנו:

                      2. מכיוון שבמקבילית, הצלעות הנגדיות שוות – נוכל להסיק שAE שווה לY (וכך היא משלימה את כל הצלע לX):

                    3. נסתכל על המשולש ABE. מהנתון שמצאנו נוכל לראות שהמשולש שווה שוקיים. נוכל להשלים את כל זוויותיו – זווית BAE שווה ל-130 (זוויות נגדיות במקבילית שוות) והזוויות בבסיס המשולש שוות כל אחת ל25 (זוויות בסיס במשולש שווה שוקיים שוות.):

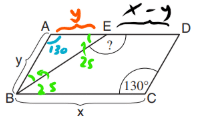
                   4. נשלים את הזווית השטוחה על הישר AD ל180, כדי למצוא את BED:
                       

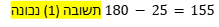
        8. נתון: 1+2b2<2+b2. איזה מהטווחים הבאים הוא הטווח המדויק ש-b יכול להימצא בו?
            תשובה (1) נכונה
            זיהוי: כפלמ”ק ואי שוויונים
            כלים רלוונטיים: נוסחאות הכפלמ”ק
            פתרון:

1. 1. נשתמש בנוסחה הראשונה של הכפל המקוצר כדי לפתוח את שני אגפי האי-שוויון:  

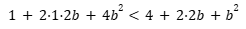
                    2. נפשט את האי שוויון
                         באמצעות סידור קוסמטי: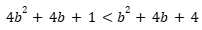 

                   3. נוריד b²+ 4b + 1  משני אגפי האי שוויון: 3b²< 3

                   4. נחלק את שני האגפים ב-3: b² < 1

                   5. מכאן ניתן להשתמש בהיגיון – b² הוא מספר חיובי קטן מ-1. אז זה אומר שהוא שבר. השורש שלו יהיה או שבר חיובי או שבר שלילי. ולכן תשובה (1) מתאימה

גרף

     9. באיזה מהזמנים הבאים היה ממוצע טמפרטורות הגוף של ארבעת הזוחלים הגבוה ביותר?
          תשובה (1) נכונה
         פתרון:  נסתכל על כל שעה ונשווה לאחרות. נשים לב שבפועל אין צורך לעשות חישוב. בשעה 13:00 הטמפרטורה של כולם היא הגבוהה ביותר אז הממוצע בהכרח יהיה הגבוה ביותר.
         

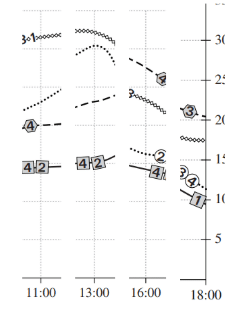
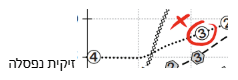
     10. אצל איזה מהזוחלים במהלך כל פרק זמן שבו טמפרטורת הגוף עלתה, רמת הפעילות עלתה או נשארה קבועה?
            תשובה (4) נכונה
            פתרון: נבדוק בנפרד כל זוחל. ברגע שנראה שהטמפרטורה עולה, אך רמת הפעילות יורדת – נפסול ונעבור הלאה.

            1.   

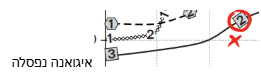
           2.

           3.

           4.

     11. ידוע שאחד הזוחלים נמצא ברמת הפעילות המרבית שלו רק למשך פרקי זמן קצרים מאוד במהלך היום. איזה מהזוחלים הוא המתאים ביותר להיות זוחל זה?
            תשובה (1) נכונה
            פתרון: נעבוד בשני שלבים קצרים. ראשית, נקבע מהי רמת הפעילות הגבוהה ביותר שכל זוחל מגיע אליה – ולאחר מכן נבדוק באומדן מי נמצא ברמת הפעילות הזו הכי מעט:

            (1) רמת הפעילות המרבית של האיגואנה היא 4. ניתן לראות שכמעט מיד לאחר שהיא עולה לרמת הפעילות הזו – היא יורדת בחזרה ל2. בסוף נגלה שהיא הכי קצרה, אך כרגע נשווה בין כל התשובות האחרות.

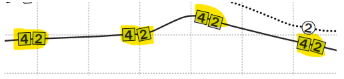
           (2) רמת הפעילות המרבית של הזיקית היא 4. ניתן לראות שזמן הפעילות שלה ברמה זו גבוה בהרבה מהאיגואנה. כבר בהתחלה. אז תשובה זו נפסלת:

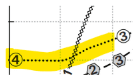
           (3) רמת הפעילות המרבית של החרדון היא 5, אך גם הוא מבלה ברמת פעילות זו יותר זמן בכל פעם מאשר האיגואנה, אז גם הוא פסול:

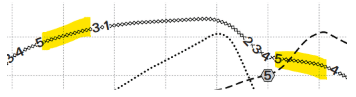
           (4) רמת הפעילות המרבית של השממית היא 5, אך גם היא מבלה פרקי זמן ארוכים ברמה זו. אז היא נפסלת:
           

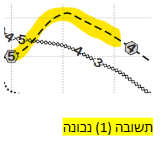
      12. על פי הנתונים שבתרשים, ככל שטמפרטורת הגוף של זוחל בתחילת היום נמוכה יותר –
             תשובה (1) נכונה
            פתרון: נבדוק כל היגד בנפרד בטבלה שממוינת על פי טמפרטורה בתחילת היום:

                    (1) כך רמת הפעילות שלו בסוף היום נמוכה יותר – נרשום את הנתונים בצורה מסודרת:

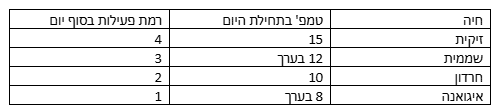
                          זה מתאים! תשובה (1) נכונה.

                    (2) כך רמת הפעילות שלו בסוף היום גבוהה יותר – גילינו בדיוק ההיפך בטבלה שיצרנו.

                    (3) כך טמפרטורת הגוף שלו בסוף היום נמוכה יותר –  נוסיף לטבלה שלנו עמודה נוספת של טמפ’ בסוף היום:

                   (4) כך טמפרטורת הגוף שלו בסוף היום גבוהה יותר – בדיוק כמו בתשובה הקודמת – אין חוקיות.

       13. איזו מהטענות הבאות נכונה בהכרח?
              תשובה (4) נכונה
              זיהוי: אותיות (ניסוח).
              כלים רלוונטיים: הצב בניסוי וטעיה.
              פתרון: ננסה לפסול תשובות באמצעות הצבות:

                    (1) אם A > 5 אז 5 > B: נציב 6 = A, 3 = B. יוצא 99 = 33 + 66. זה עובד. זו תשובה קצת כללית אז ננסה לפסול את האחרות.

                    (2) אם B = A אז 5 > C: את זה קל לפסול. נציב 4 = B,A ונקבל 88 = 44 + 44. התשובה נפלה.

                   (3) B + A > 5: נציב הצבה דומה למקודם (1 = B,A) ונקבל תוצאה הגיונית. התשובה נופלת.

                   (4) B + A > C: נשתמש באותה הצבה כמו ב(2) והתוצאה תקינה. C = 8 = B + A. התשובה נפלה.

                    פסלנו 3 תשובות אז תשובה (1) נכונה!

       14. בכמה דרכים אפשר לסדר את הכדורים בשורה כך שהשחור והלבן יהיו זה לצד זה וגם האדום והירוק יהיו זה לצד זה?
              תשובה (2) נכונה
              זיהוי: קומבי (בכמה דרכים אפשר לסדר)
             כלים רלוונטיים: עבודה ידנית
             תשובות: מספרים קטנים מ-16. נעבוד ידנית.
             פתרון: יש לנו שתי זוגות שחייבים להיות אחד ליד השני. נתחיל עם כל הסידורים האפשריים כשהשחור והלבן בצד ימין:
             ש-ל–י–א, ש-ל–א–י
             ל-ש-י–א, ל-ש-א–י
             נמשיך למצבים בהם השחור והלבן בצד השני:
            י–א-ש-ל, י–א–ל-ש
           א–י-ש-ל, א–י–ל-ש
          סה”כ 8 אופציות. תשובה (2) נכונה

      15. מה שטחו של עיגול שאורך הרדיוס שלו שווה לאורך המקצוע של קובייה ששטח פניה 18 סמ״ר?
             תשובה (3) נכונה
             שאלת גיאומטריה – שרטוט: אין שרטוט, אך אין צורך לשרטט. מדברים על תלת ממד ועל עיגול.
             שאלה: רוצים מאתנו את השטח של העיגול (r2)
            תשובות: כולן בπ
           פתרון: 

1. 1. נתון ששטח הפנים של הקובייה הוא 18 סמ”ר. מכיוון שבקוביה כלל הםאות שוות – נחלק את שטח הפנים ב-6 כדי לקבל שטח של פאה אחת:
   2. כדי למצוא את מקצוע הקוביה – נוציא שורש משטח הפאה שמצאנו (כל פאה בקובייה היא ריבוע):  
   3. היות והמקצוע שווה לרדיוס העיגול – נציב אותו בנוסחת השטח:
       תשובה (3) נכונה.

                    הערה חשובה: יש להקפיד על רישום מסודר בשאלה זו – יש סיכוי להתבלבל בין המקצוע לשטח הפאה, ואז תשובה (1) הופעת למסיח.

       16. למה שווה X?
              תשובה (3) נכונה
              זיהוי: תנועה (החתול והשער נעים במרחב במהירות וזמן מוגדרים)
             כלים רלוונטיים: טבלת מז”ד, הרמת יחידות.
             תשובות: מספרים
             פתרון: אנחנו רוצים למצוא את מהירות החתול. נשבץ את כל הנתונים שבשאלה בטבלת מז”ד ונשים לב שהשער עבר 120 ס”מ (רוחב הפתח היה 180)

          מכאן נוכל להשלים את הזמן של השער באמצעות חילוק במהירות: 12=120/10. היות והחתול עבר בשער באותו זמן, נשבץ את הנתון גם אצלו:
         

          מכאן נחשב: 5 = 60/12. תשובה (3) נכונה

       17. למה שווה X?
              תשובה (4) נכונה
              זיהוי: שאלה כללית (על דרך השלילה, אין כאן תבנית מוכרת)
              תשובות: שברים עשרוניים
             פתרון: 

1. 1. נסמן אותיות מייצגות: דינר = D. פרנק = F. לירות = L.
   2. נבנה משוואות מהנתונים:
   3. נשתמש בבידוד והצבה כדי לפתור את מערכת המשוואות: F מבודד במשוואה הראשונה אז נציב אותו בשלישית: 4Lx = 9D.
   4. D מבודד במשוואה השנייה, אז נציב אותו גם כן במשוואה: 4Lx = 9⋅3.6L.
   5. נחלק את שני אגפי המשוואה בL כך שנישאר רק עם X ומספרים: 4x = 9⋅3.6 
   6. נפתור את האגף הימני: 4x = 27 + 5.4 = 32.4
   7. נחלק את שני האגפים ב-4: x = 8.1. תשובה (4) נכונה.

      18. פי כמה גדל המספר?
             תשובה (3) נכונה
             זיהוי: שאלת אחוזים (הגדילו ב%)
            כלים רלוונטיים: טיפים באחוזים
            תשובות: במספרים
            פתרון: נתון מספר חיובי, אך לא ציינו לנו איזה – מה שמאפשר לנו להציב מספר מהראש. נחליט על אחד כי הוא הקטן ביותר החיובי. כדי לבדוק בכמה תכלס הגדילו נבדוק כמה זה 4000% מתוך 1. נוכל להשתמש בטיפ שירותים כדי להוריד שני אפסים ונקבל: 40⋅1=40.
            נקבל 41 = 1 + 40. תשובה (3) נכונה

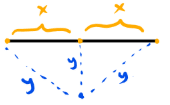
       19. כמה נקודות כאלה תוכל תמר לצייר?
              תשובה (4) נכונה
              גאומטריה – שרטוט: אין שרטוט. נשרטט בעצמנו.
              תשובות: מספרים, אינסוף ו-0.
              פתרון: 

1. 1. נצייר את שלושת הנקודות במישור(בכתום), ונקבע נקודה נוספת באמצע המישור שמרחקה מהנקודות היא Y(בכחול):
      
2.              

                   2. נוצרו לנו משולש שווה שוקיים גדול כשבפועל כל אחד מהמשולשים הקטנים שמרכיבים אותו הוא גם שווה שוקיים. מכאן נסיק מסקנות על 2 מצבים: במצב הראשון. הקו במרכז אנך למישור ונוצר השרטוט הבא:

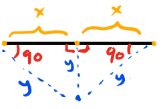
                         שרטוט זה אינו הגיוני. היות וסכום הזוויות בכל משולש יעלה על 180.

                     3. המצב השני: במידה ונזיז את הנקודה הכחולה לאחד הצדדים, הדבר יהיה כרוך בהכרח בשינוי אורכי אחד מהקווים. לדוגמה:

                    4. היות ולא מצאנו מקרה אחד אפשרי למיקום הנקודה. התשובה היא 0. כלומר תשובה (4)

       20. כמה מחלקים שונים זה מזה יש למספר A (כולל 1 ו-A עצמו)?
              תשובה (4) נכונה
              זיהוי: חלוקות (שואלים על מחלקים)
              כלים רלוונטיים: מציאת מחלקים, הצבת מספרים מהראש
              תשובות: חלקן בנעלמים.
              פתרון: נציב בנעלמים את המספרים הראשוניים 2, 3, ו5. המכפלה שלהם היא A = 30. נמצא את המחלקים של 30: 1, 2, 3, 5, 6, 10, 15, 30. סה”כ 8. תשובה (4) מתאימה, אך נוודא שתשובות (1) ו(2) עם הנעלמים לא יצאו אותו דבר:

1. 1. 30/3 = 10
   2. 30/2 = 15

                   תשובה (4) נכונה