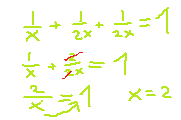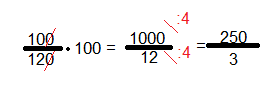פתרון בחינת אביב 2023 פרק כמותי 2

תשובה נכונה: 1

זיהוי: מעגל, שטח משולש.

כלים רלוונטיים: כל הרדיוסים במעגל שווים אחד לשני. שטח משולש זה בסיס כפול גובה חלקי 2

הסבר:

אחד כפול 2 חלקי 2 זה 1.

תשובה 1.

תשובה נכונה: 2

זיהוי: קושיות- עברית למתמטית, הצבות.

כלים רלוונטיים: שואלים שאלה ספציפית, למה שווה X. מתחיל בהצבה של מספר נוח.

הסבר: אם נציב 2 בתור ה-X. יצא שאסף אכל חצי מהעוגה, מלי אכלה רבע וניקול גם. אכן יוצא עוגה שלמה.

אפשר גם אלגברית:

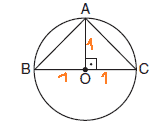
תשובה נכונה: 1

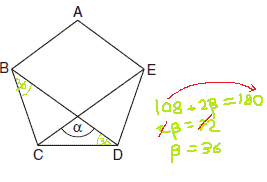
זיהוי: משוכללים (בגלל המחומש)

כלים רלוונטיים: זווית מחומש פנימית שווה ל108 מעלות.

הסבר: נתחיל מלהתמקד במשולש BCD, הוא שווה שוקיים, וזווית C שווה ל108.

זווית D ו-B שוות זו לזו ול36. בגלל החישוב הבא:

אותו הדבר מתרחש גם במשולש ECD, זווית C גם שווה ל36.

זווית אלפא משלימה 180 מעלות במשולש, לכן שווה ל108.

תשובה 1.

תשובה נכונה: 4

זיהוי: שורשים

כלים רלוונטיים: חזקים לשמיים שורשים לאדמה! (ניתן לצמצם חזקה ושורש).

הסבר: נצמצם את החזקה והשורש ואז נעלה בריבוע:

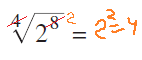
תשובה 4.

תשובה נכונה: 3

זיהוי: יחסים בתנועה.

כלים רלוונטיים: אם הדרך התקצרה נחלק, אם הזמן התארך, גם נחלק (אם עברת פחות מרחק וזה לקח יותר זמן, נסעת לאט יותר)

הסבר: עודד עבר דרך קצרה פי 2 בפי 3 זמן, ז”א נאלץ להכפיל את מהירותו פי 2 ואז פי 3 כדי שיגוע למהירות של תמר.

נכפיל פי 6

תשובה 3.

תשובה נכונה: 4

זיהוי: פירוק לגורמים

כלים רלוונטיים: נתחיל לפרק את המספרים לגורמים שלהם עד שנצליח להרכיב כל אחת מהתשובות

הסבר: נתחיל בפירוק לגורמים:

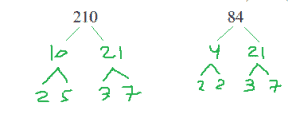
עכשיו נבדוק אילו מספרים אפשר ליצור מה”רכיבים” האלה:

• קיים בשניהם, ז”א מחלק את שניהם
• 2*3=6 ואפשרי בשני המספרים
• קיים בשניהם, ז”א מחלק את שניהם
• קיים רק ב84, תשובה נכונה.

תשובה נכונה: 4

זיהוי: קושיות כלליות, איקאה.

כלים רלוונטיים: ציור ברור של הסיטואציה

הסבר: בפרח יש 10 מ”ל, נצייר מה קורה עם כל דבורה בכל דקה:

נראה שהן שתו 10 מ”ל לאחר שהגיעה הדבורה הרביעית. הדבורה הראשונה הספיקה לשתות 4 מ”ל.

תשובה נכונה: 4

זיהוי: מספרים עוקבים

כלים רלוונטיים: הצבה!

הסבר: נציב 2 ו-3 ונראה מה יוצא:

2*2 – 3 = 1

• פוסלים
• נכון
• פוסלים
• נכון

שתי תשובות נכונות, בואו ננסה הצבה נוספת, 3 ו- 4.

2*3 – 4 = 2

עכשיו גם תשובה 2 לא נכונה.

תשובה 4.

תשובה נכונה: 3

זיהוי: מספרים עוקבים, אותיות.

כלים רלוונטיים: הצבה!

הסבר: נציב 1,2,3,4

12+34=46 עובד!

נציב 2,3,4,5

23+45=68 עובד!

נציב 3,4,5,6

34+56=90 גם עובד!

אנחנו רואים מראש שההצבה הבאה לא תעבוד (המספר יהיה כבר תלת ספרתי).

3 ערכים אפשריים סה”כ.

תשובה 3.

תשובה נכונה: 1

זיהוי: קושיות- איקאה.

כלים רלוונטיים: הצבה.

הסבר: גם כאן שואלים שאלה ספציפית, ומומלץ מאוד להציב.

ההצבה הנוחה ביותר היא 2 (קטן) אבל אם נציב את זה נראה שלאחר 8 תורות הוא יגיע למקסימום 16.

ההצבה השנייה הכי נוחה היא 5. אם הוא ניצח בכל 8 הפעמים היה מקבל 40 (8*5). אם ניצח 7 פעמים יקבל 34 (7*5-1). אם ינצח 6 פעמים ויפסיד פעמיים ייקבל בול 28 (5*6-2).

תשובה 1.

תשובה נכונה: 3

זיהוי: תלת מרחב- גליל

כלים רלוונטיים: שטח המעטפת של גליל הוא 2πR*h, והנפח הוא πR²*h

הסבר: שואלים על נפח, אז אנחנו צריכים גובה ורדיוס, גובה כבר נתון (3).

נמצא את הרדיוס באמצעות נוסחת שטח המעטפת:

2πR*3=6 נצמצם 3 ו-2 עם ה-6:

πR=1 עכשיו נבודד את הרדיוס (נחלק בפאי):

R=1/π.

עכשיו נציב את הנתונים בנוסחת הנפח:

π (1/π)² *3= π *(1/π²)*3

אחרי צמצום של הפאי נקבל:

3/ π

תשובה 3.

תשובה נכונה: 3

זיהוי: אחוזים

כלים רלוונטיים: הצבה, כדי לעבור משבר לאחוז עלינו להכפיל פי100. 

הסבר: נציב 100 בתור y ונראה שה-x יהיה שווה ל120.

שואלים לכמה אחוזים מ-x שווה הy,

Y מתוך x שווה ל:

זה השבר, על מנת להמיר את זה לאחוזים עלינו להכפיל פי 100:

      נמשיך בצמצום (כמה פעמים נכנס 3 ב250). נראה שנכנס 80 פעמים בצורה נוחה:

      נכנס עוד 3 פעמים:

      תשובה 3.

תשובה נכונה: 1

זיהוי: גיאומטריה, שטחים

כלים רלוונטיים: שטח מקבילית שווה לממוצע הבסיסים כפול גובה.

הסבר: היקף הריבוע הוא 12, ז”א שכל צלע היא 3. נתחיל בלסמן את הנתונים על גבי הצורה, שימו לב שאומרים לנו שהטרפזים בצדדים חופפים (זהים):

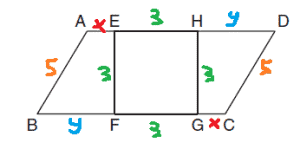
אם ההיקף של המקבילית הוא 28, אפשר להציב:

2x+2*3+2*y+2*5=28

נחלק הכל פי 2:

X+3+y+5=14

נעביר את ה-3 וה-5 לצד השני ונקבל:

x+y=6

ז”א שצלע AD וצלע BC (וגם הממוצע ביניהן) שוות ל-9 כל אחת. (כי הן שוות לx+y+3).

הגובה שווה לצלע הריבוע, 3. נחשב את שטח המקבילית ABCD:

3*9=27

המקבילית מורכבת מהריבוע EFGH ומהטרפזים ABFE ו- HGCD. שטח הריבוע באמצע שווה ל-9 (צלע הריבוע בריבוע), ז”א ששני הטרפזים בקצוות שווים ל18 ביחד, ז”א שכל אחד מהם שווה ל-9.

תשובה 1.

תשובה נכונה: 2

זיהוי: דמיון משולשים

כלים רלוונטיים: יחסים במשולשים דומים, שרטוט.

הסבר:

מתוארים לנו שני משולשים דומים, עם גודל צלעות שונה, נשרטט:

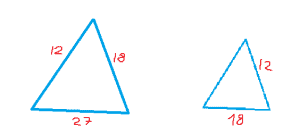
יחס הצלעות בשנני המשולשים הוא:

12:18:27

נחלק ב-3 (כי יחס טוב הוא יחס מצומצם).

4:6:9

נביט במשולש השני, כי להגיע ל-12 ו-18 עלינו להכפיל את היחס פי 2 (ולא פי 3 כי אחרת נחזור לאותו המשולש). נקבל:

8:12:18

ז”א הצלע הנותרת שווה ל8.

תשובה 2.

תשובה נכונה: 1

זיהוי: קושיות, איקאה.

כלים רלוונטיים: הצבה, ציור

הסבר: נציב מספר כלשהו (לא משנה איזה) ונראה שהתסריט הזה אפשרי רק אם כל 4 המספרים הם זהים, כי אחרת לא יכול להיות שכל המספרים יהיו ממוצע של ה”שכנים” שלהם.

תשובה 1.

תשובה נכונה: 3

זיהוי: גרפים

כלים רלוונטיים: נבדוק איפה גרף המכירות “עולה”.

הסבר: נביט בגרף ונסמן את כל המקטעים העולים:

סך הכל 3 שנים, תשובה 3.

תשובה נכונה: 1

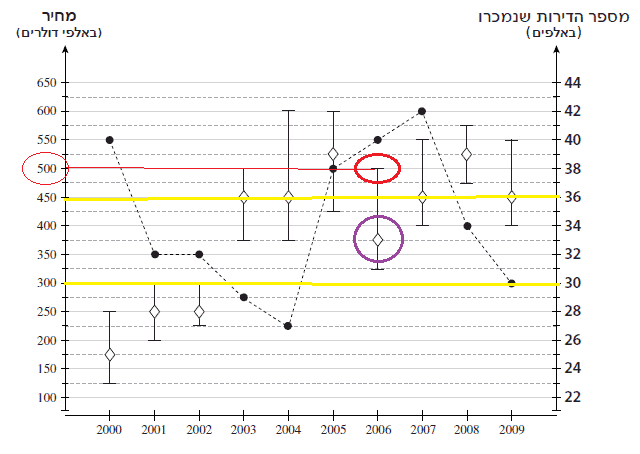
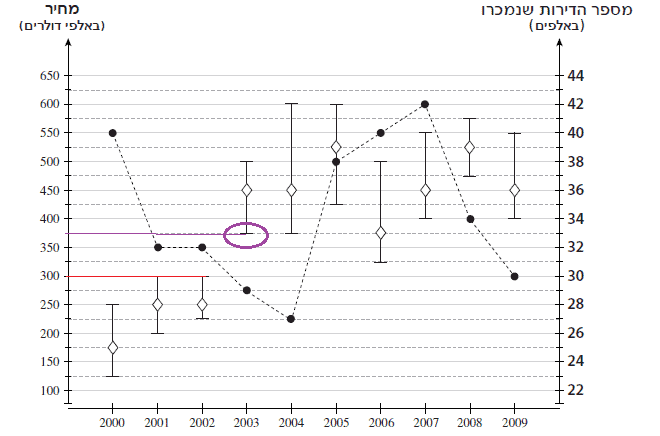
זיהוי: גרפים

כלים רלוונטיים: נסמן את הגבולות של הטווח שמציגים ונבדוק מה המחיר בטווח העליון.

הסבר: נסמן “גבולות גזרה” בדף:

נוכל לראות שהיא קנתה את הדירה ב-2006.

עכשיו נסמן את מחיר הדירות היקרות:

תשובה 1.

תשובה נכונה: 3

זיהוי: גרפים

כלים רלוונטיים: אורך הקו הוא למעשה ההפרש שבין המחיר היקר לזול.

הסבר: נדגיש ונחשב את אורכם של כל הקווים על מנת להבין מי הכי ארוך ומי הכי קצר

(הפיזור) כל קו שווה ל25,000 דולר:

המנה מהחלוקה של שניהם תהיה 3.

תשובה 3.

תשובה נכונה: 1

זיהוי: גרפים

כלים רלוונטיים: נחפש איפה הקו התחתון (שמסמן את המחיר של הדירות הזולות שנמכרו) יותר גבוה מכל הקווים העליונים (שמסמן את מחיר הדירות היקרות) שבאו בשנים שלפניו.

הסבר: נחפש בגרף איפה מתקיים התנאי הזה ונסמן:

רואים שב2003 זה היה המצב המתואר, בכל השנים שלפני זה אפילו הדירות הכי יקרות היו יותר זולות מהדירה הכי זולה ב2003. נבדוק כמה דירות נמכרו באותה שנה ונקבל 27,000.

תשובה 1.

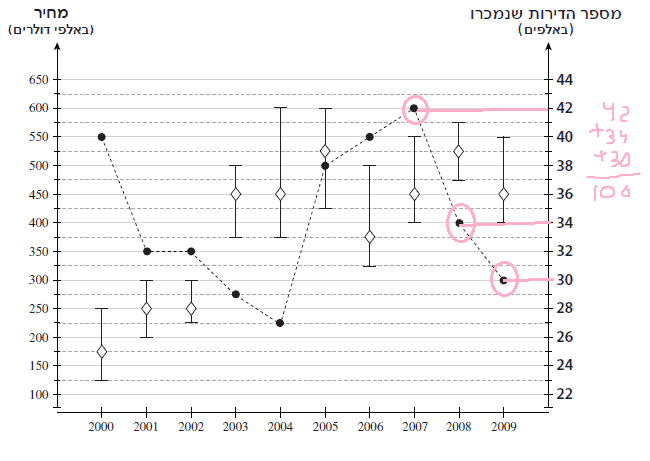
תשובה נכונה: 4

זיהוי: גרפים

כלים רלוונטיים: אם הדירות היקרות והזולות הן 25% כל אחת, אז 50% מהדירות לא נמצאות באף אחת מהקטגוריות האלה.

הסבר: נסמן את השנים שעליהן מדובר ונראה כמה דירות נמכרו בהן:

נראה שסך הדירות שנמכרו הוא 106 אלף, 50 אחוז מהן זה 53 אלף.

               תשובה 4.