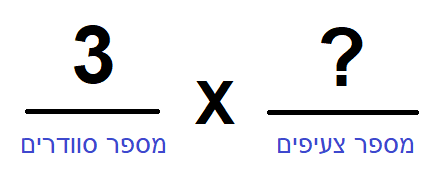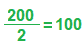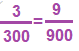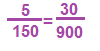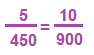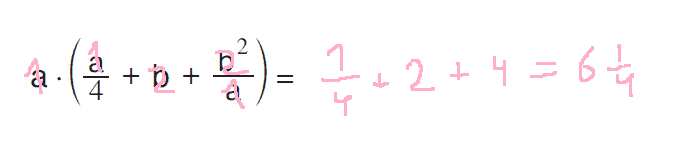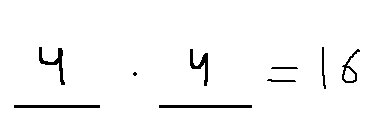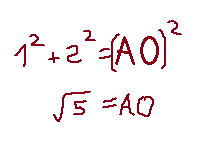פתרון בחינת אביב 2023 פרק כמותי 1

בסרטוט שלפניכם שתי קרניים היוצאות מנקודה אחת.

תשובה נכונה: 1

זיהוי: גיאומטריה- זויות (כי זה כל מה שקיים בשאלה)

כלים רלוונטיים: זווית “שלמה” (מעגל) שווה ל360. “קרמבו” (אפשר להציב משתנה אחד במקום אותו המשתנה במשוואה אחרת.

הסבר: אם נחבר את שתי הזויות אלפא וביטא נראה שנוצר לנו מעגל.

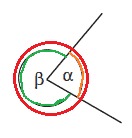
בצורת משוואה:

a+b=360

אם ניזכר במשוואה שנתונה לנו, b=5a. נוכל להציב במקום ה-b במשוואה הראשונה 5a ונקבל:

a+5a=360

ז”א:

6a=360

נחלק ב-6 משני הצדדים ונקבל:

a=60

תשובה 1.

הצבה: אם רוצים, אפשר גם להציב את תשובה מספר אחת כיוון שמדובר בהצבה נוחה ויפה. נראה שלפי ההצבה b=300 וביחד זה נותן 360, מתאים!

2.

תשובה נכונה: 2

זיהוי: שאלת קושיות כללית (כי לא מתאים לאף תבנית אחרת)

כלים רלוונטיים: ציור של המספרים

הסבר: ספרת העשרות גדולה פי 2 מהאחדות, אז בואו נחשוב מה הספרת עשרות הכי גדולה שיכולה להיות: 9, אבל תשע לא זוגי אז לא יכול להיות גדול פי2, נלך על 8. ספרת האחדות קטנה פי 2 אז המספר הוא 84.

המספר הקטן ביותר שמקיים את התנאי יהיה 21.

ההפרש ביניהם: 84-21=63.

תשובה 2

תשובה נכונה: 2

זיהוי: הספק (כי עושים עבודה כלשהי בזמן כלשהו)

כלים רלוונטיים: עבודה שמבוצעת יחד זה סכום ההספקים (עבודה חלקי זמן)

הסבר: נצייר-

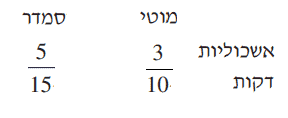
נעשה מכנה משותף (30):

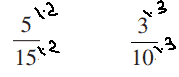
קיבלנו 19 אשכוליות בשלושים דקות (חצי שעה). שואלים לגבי שעתיים אז צריך עוד להכפיל ב-4.
נקבל 76.

תשובה 2

תשובה נכונה: 4

זיהוי: אלגברה (מספרים, נעלמים ומשוואות)

כלים רלוונטיים: גולאג (חיבור או חיסור משוואות שלמות).

הסבר: כאשר נותנים לנו שתי משוואות, כמעט ותמיד נאלץ או לחבר או לחסר אותן. המטרה לרוב היא “להעלים” את אחד הנעלמים. בשאלה הזו מופיעים שני הנעלמים, אז אין צורך להעלים אותם.

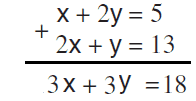
נחלק ב-3 את כל הגורמים:

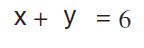
תשובה 4.

תשובה נכונה: 3

זיהוי: קומבי (שואלים על צירופים)

כלים רלוונטיים: כמות הצירופים האפשרית שווה למכפלת כל האירועים.

הסבר: אם יש לנו 7 צירופים, ואנו יודעים שיש שני אירועי בחירת בגד: סוודר וצעיף.

עלינו להכפיל ביניהם:

כל התשובות יתנו יותר מ-7, אבל שואלים לכל הפחות, אז:

תשובה 3.

תשובה נכונה: 4

זיהוי: סמי בורקס, שטח משולש

כלים רלוונטיים: ניצבי סמי בורקס שווים ליתר חלקי שורש 2.

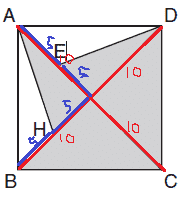
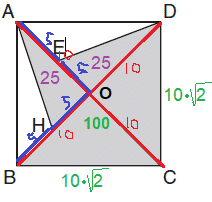
הסבר: נתחיל בלסמן את כל אורכי הצלעות שאמרו לנו למה הם שווים.

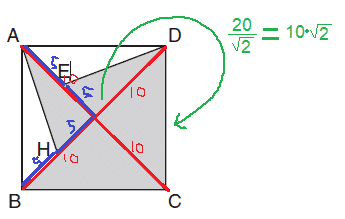
עכשיו נחשב את צלע הריבוע (היא הניצב בסמי בורקס):

חילקנו באמצעות רובין הוד הפוך, חילקנו 20 ב-2 והכפלנו במה שיש למטה.

נחשב את שטח המשולש BDC, גובה כפול בסיס חלקי 2:

עכשיו נחשב את שני המשולשים הזהים AHO ו-DEO.

100+25+25= 150

תשובה 4.

תשובה נכונה: 2

זיהוי: חלוקות

כלים רלוונטיים: מספק שמתחלק ב10 יסתיים ב-0.

הסבר: יש חמישה אנשים, כך שכל פעם שכולם מקבלים זוג “הולכים” 10 קלפים. אם זה יקרה 10 פעם, יישארו רק 4 קלפים מ104 שהיו (ילכו 100). שניים ממה שנותר יקבל א’, ואת השניים האחרונים יקבל ב’.

תשובה 2.

תשובה נכונה: 1

זיהוי: “משפחות” (תשובות עם טווח מזפרים)

כלים רלוונטיים: במכפלה של מספרים, מה שמקטין את המכפלה זה או כפל בשלילי או כפל בשבר.

הסבר: Y חייב להיות חיובי כי הוא גדול מערך מוחלט.

בואו נביט כיצד משפיע הX על הY, כי הY זה מה שקבוע בשלוש הביטויים.

בלי הX, הY יהיה הכי גדול. אם מכפילים באיקס, הוא קטן. אבל הוא קטן פחות אם שמים לו ערך מוחלט, ז”א שהוא שלילי.

אם אנחנו יודעים שהוא מקטין אם מכפילים בו גם עם ערך מוחלט אז הוא חייב להיות שבר.

שלילי ושבר? תשובה 1.

תשובה נכונה: 2

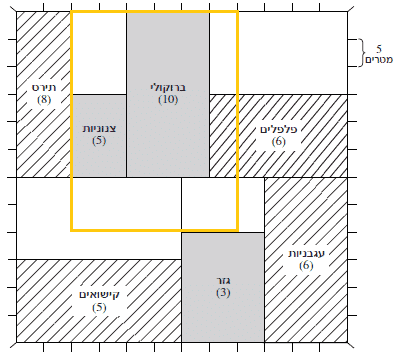
זיהוי: גרף

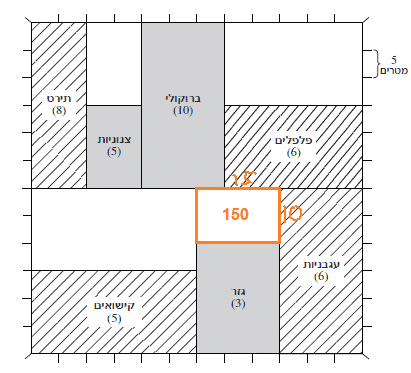
כלים רלוונטיים: שטח מלבן זה צלע כפול צלע.

הסבר: ליד העגבניות יש רק חלקה אחת ריקה שצלעותיה הן 10 על 15.

תשובה 2.

תשובה נכונה: 3

זיהוי: כפל וחלוקה, יחס.

כלים רלוונטיים: אם שואלים פי כמה גדול משהו ממשהו אחר צריך לחלק ביניהם.

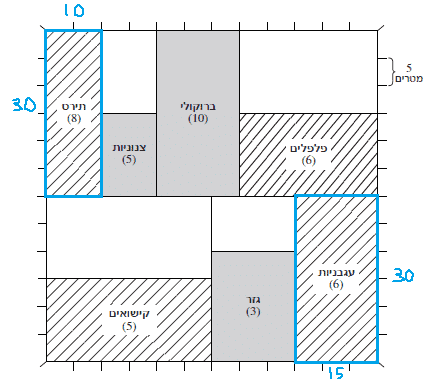
הסבר: נכפיל את שטח החלקה ביחסי המים (את העגבניות נכפיל פי 2):

חלקת העגבניות היא 30 כפול 15, ז”א 450.

חלקת התירס היא 30 כפול 10, ז”א 300.

נחלק את שטח העגבניות כפול 2 בחלקת התירס:

תשובה 3.

תשובה נכונה: 2

זיהוי: חילוק

כלים רלוונטיים: ליצירת מכנה משותף מכפילים את הלמעלה והלמטה על שהמכנה יהיה זהה בין כל השברים. השבר עם המונה הגדול ביותר הוא הגדול ביותר.

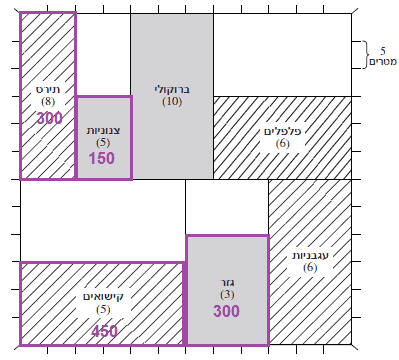
הסבר: נבדוק את היחס בכל אחת מהתשובות, מחנה משותף 900.

1. גזר:

2. צנונית:

3. קישוא:

4. תירס:

12.

תשובה נכונה: 2

זיהוי: חיסור

כלים רלוונטיים: לצייר על גבי השרטוט!

הסבר: 30 על 40 מטר זה 6 על 8 משבצות, נצייר:

השטח הכי גדול שאפשר לכסות בגידולי החורף מכסה את הברוקולי והצנוניות, אבל משאיר את חלקת הגזר (300) חשופה.

תשובה 2.

תשובה נכונה: 1

זיהוי: אלגברה

כלים רלוונטיים: יש פה משתנה שלא מתפנה, נציב!

הסבר: נציב a=1, b=2.

קודם, נציב בתרגיל המקורי:

עכשיו נבדוק את שאר התשובות:

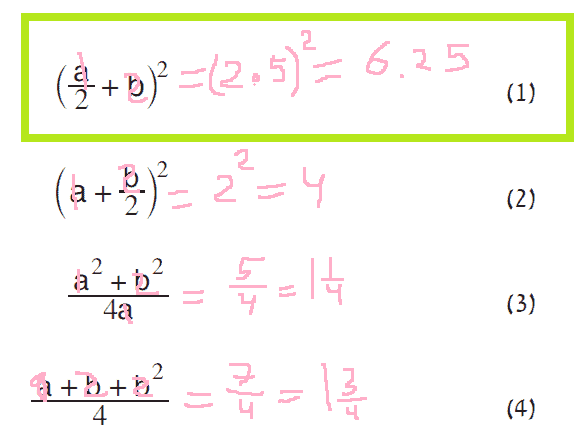
תשובה 1.

תשובה נכונה: 4

זיהוי: ממוצע

כלים רלוונטיים: הערכת סדר גודל

הסבר: ממוצע זה הסכום חלקי מספר המשתתפים.

כיוון שכל המספרים פה לא מוגבלים, הממוצע יכול להיות גם מיליון וגם מינוס מיליארד.

תשובה 4.

תשובה נכונה: 1

זיהוי: ציר מספרים

כלים רלוונטיים: אם אחד מערכי ה-X או ה-Y שווים לראשית הצירים (0,0) הנקודה נמצאת על הציר.

הסבר: אם נתון לנו שערכי האיקס של נקודה B שווים ל-0, הנקודה B נמצאת על הישר Y.

אם נתון לנו שערכי הוואי של נקודה A  שווים ל-0, הנקודה A נמצאת על הישר X.

נצייר ונראה את התשובה:

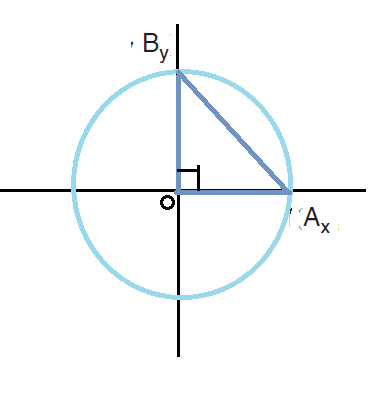
משולש ישר זווית, תשובה 1.

תשובה נכונה: 1

זיהוי: אחוזים

כלים רלוונטיים: אם אין מספר ורק אחוזים נציב 100! (100 לשירותך).

הסבר: נציב 100 בסכום של יום ראשון ונצייר את השינוי בכל אחד מהימים. שאלו אותנו מתי המחיר עולה ב10% מעל המחיר המקורי (שבו הצבנו 100), אז אנחנו מחפשים את היום שבו נעבור את ה-110

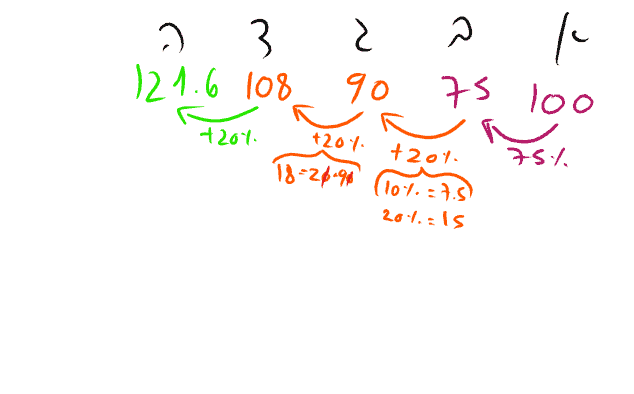
ניעזר בטיפ שירותים ומלצרים כדי לחשב את השינוי בכל אחד מהימים.

רואים שהמחיר עולה מעל ה-110 המקורי ביום חמישי (הערה – חישבנו במקרה הזה את השינוי מיום רביעי לחמישי אך אין בכך צורך באמת. ניתן להסיק לפי השינוי בימים שלפני שנעבור את ה110 גם בלי חישובים).

תשובה 1.

תשובה נכונה: 2

זיהוי: הסתברות (לפי מילת השאלה).

כלים רלוונטיים: הסתברות זה מספר האופציות הרצויות חלקי כל האופציות שייתכנו.

הסבר: נתחיל בלהבין כמה אופציות יש סך הכל (באמצעות קומבי) יש שני אירועים (שתי הטלות) ובכל הטלה יש 4 אפשרויות (כי בפירמידה יש 4 פאות):

עכשיו נחשב כמה אפשרויות רצויות יש מבחינתנו (כדי שהסכום יהיה 4):

מתאים לנו או 2 ו-2 או 1 ו-3 או 3 ו-1, שלוש אפשרויות סך הכל.

אז הרצוי חלקי המצוי יהיה 3 חלקי 16.

תשובה 2.

תשובה נכונה: 3

זיהוי: מכפלה

כלים רלוונטיים: שטח מלבן זה צלע כפול צלע.

הסבר: בודקים מה מהמספרים ניתן להכפיל במשהו כדי לקבל 91 (למעשה שואלים במה מהתשובות מתחלק 91.

1. 91 לא מתחלק ב-9
2. 91 לא מתחלק ב-11
3. 91 אכן מתחלק ב13 לקבלת.
4. דווקא אפשר.

19.

תשובה נכונה: 1

זיהוי: מעגל, משולש

כלים רלוונטיים: משפט פיתגורס.

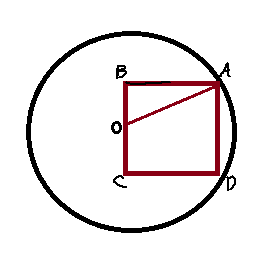
הסבר: נשרטט, אנחנו רוצים ש”הנקודה” תהיה כמה שיותר רחוקה מהנקודה O, ז”א באחת מפינות הריבוע הרחוקות:

צלע BC שווה ל-2 וצלע BO שווה לחצי מזה, ז”א 1.

על מנת לחשב את היתר, נעשה פיתגורס:

תשובה 1.

תשובה נכונה: 1

זיהוי: הכל בדולר

כלים רלוונטיים: נציב מספר בנוסחה.

הסבר: שואלים איזה מהנוסחאות שבתשובות בעצם משאירה את המספר כמו שהוא אם עושים את הפעולה פעמיים.

1. חזקה שלילית פשוט הופכת את המונה והמכנה, אם נעשה את זה פעמיים אכן נגיע לאותו המספר.
2. חזקת חצי עושה שורש, שורש פעמיים כמובן לא מבטל את פעולת השורש. למרות שהמינוס כן “מתבטל”.
3. אפשר להציב 2 ולראות שלא עובד.
4. אם מחלקים משהו ב2 פעמיים ואז מעלים אותו בריבוע פעמיים הוא לא בטוח יחזור למה שהיה.